Facies Prediction from Well Logs - Neural Network Model Hyper-Parameters Optimisation
In this project, we will implement standard and comprehensive steps to select the best model and hyper prameters to predict rock facies form a dataset. First, we will prepare data for modeling, fit the models and cross validate, predict facies labels and evaluate prediction accuracy by several model evaluation metrics. Finally, we will examine model performance on blind-well data. These are the models that we will use:
1 - Logistic Regression Classifier
2 - K Neighbors Classifier
3 - Decision Tree Classifier
4 - Random Forest Classifier
5 - Support Vector Classifier
6 - Gaussian Naive Bayes Classifier
7 - Gradient Boosting Classifier
8 - Extra Tree Classifier
The dataset for this study comes from Hugoton and Panoma Fields in North America. It consists of log data (the measurement of physical properties of rocks) of nine wells. We will use these log data to train supervised classifiers in order to predict discrete facies groups. For more detail, you may take a look here. The seven features are:
GR: this wireline logging tools measure gamma emission
ILD_log10: this is resistivity measurement
PE: photoelectric effect log
DeltaPHI: Phi is a porosity index in petrophysics.
PNHIND: Average of neutron and density log.
NM_M:nonmarine-marine indicator
RELPOS: relative position
The nine discrete facies (classes of rocks) are:
(SS) Nonmarine sandstone
(CSiS) Nonmarine coarse siltstone
(FSiS) Nonmarine fine siltstone
(SiSH) Marine siltstone and shale
(MS) Mudstone (limestone)
(WS) Wackestone (limestone)
(D) Dolomite
(PS) Packstone-grainstone (limestone)
(BS) Phylloid-algal bafflestone (limestone)
The project content:
1- Data Exploratory Analysis¶
1-1 Data visualization
1-1-1 log-plot
1-1-2 Bar plot
1-1-3 Cross-plot1-2 Feature Engineering
1-2-1 NaN imputation
1-2-2 Feature extraction
1-2-3 Oversampling1-3 Feature Importance
1-3-1 Feature linear corrolation
1-3-2 Decision tree
1-3-3 Permutation feature importance
2- Build Model & Validate¶
2-1 Baseline Model
2-2 Hyper-parameters2-2-1 Grid search
3- Model Evaluation-1¶
3-1 Model Metrics
3-2 Confusion matrix
4- Model Evaluation-2¶
4-1 Learning curves
4-2 ROC plot
4-3 Blind well prediction and evaluation
1 Data Exploratory Analysis¶
After data reading into python using Pandas, we can visualize it to understand data better. Before plotting, we need to define a color map(this step deserves to be in the Feature engineering part but we need here to plot color for facies classes) and devote color code for each facies.
Note1: codes embedded in this manuscript are presented to understand the work procedure. If you want to exercise by yourself, I highly recommend using the jupyter notebook file.
Note2: shuffling data can cause differences between your runs and what appears here.
import pandas as pd
import matplotlib.colors as colors
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable
from sklearn.preprocessing import LabelEncoder
from collections import Counter
pd.set_option('display.max_rows', 30)
import numpy as np
import seaborn as sns
from sklearn.metrics import accuracy_score
df = pd.read_csv('facies_vectors.csv')
df.tail()
| Facies | Formation | Well Name | Depth | GR | ILD_log10 | DeltaPHI | PHIND | PE | NM_M | RELPOS | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4144 | 5 | C LM | CHURCHMAN BIBLE | 3120.5 | 46.719 | 0.947 | 1.828 | 7.254 | 3.617 | 2 | 0.685 |
| 4145 | 5 | C LM | CHURCHMAN BIBLE | 3121.0 | 44.563 | 0.953 | 2.241 | 8.013 | 3.344 | 2 | 0.677 |
| 4146 | 5 | C LM | CHURCHMAN BIBLE | 3121.5 | 49.719 | 0.964 | 2.925 | 8.013 | 3.190 | 2 | 0.669 |
| 4147 | 5 | C LM | CHURCHMAN BIBLE | 3122.0 | 51.469 | 0.965 | 3.083 | 7.708 | 3.152 | 2 | 0.661 |
| 4148 | 5 | C LM | CHURCHMAN BIBLE | 3122.5 | 50.031 | 0.970 | 2.609 | 6.668 | 3.295 | 2 | 0.653 |
# specify some data types may python concern about
df['Facies'] = df['Facies'].astype('int')
df['Depth'] = df['Depth'].astype('float')
df['Well Name'] = df['Well Name'].astype('category')
# colors
facies_colors = ['xkcd:goldenrod', 'xkcd:orange','xkcd:sienna','xkcd:violet',
'xkcd:olive','xkcd:turquoise', "xkcd:yellowgreen", 'xkcd:indigo', 'xkcd:blue']
facies_labels = ['SS', 'CSiS', 'FSiS', 'SiSh',
'MS', 'WS', 'D','PS', 'BS']
#facies_color_map is a dictionary that maps facies labels to their respective colors
facies_color_map = {}
for ind, label in enumerate(facies_labels):
facies_color_map[label] = facies_colors[ind]
def label_facies(row, labels):
return labels[ row['Facies'] -1]
#establish facies label str
df.loc[:,'FaciesLabels'] = df.apply(lambda row: label_facies(row, facies_labels), axis=1)
data=df
This is function to create a plot.
def make_facies_log_plot(logs, facies_colors):
#make sure logs are sorted by depth
logs = logs.sort_values(by='Depth')
cmap_facies = colors.ListedColormap(
facies_colors[0:len(facies_colors)], 'indexed')
ztop=logs.Depth.min(); zbot=logs.Depth.max()
cluster=np.repeat(np.expand_dims(logs['Facies'].values,1), 100, 1)
f, ax = plt.subplots(nrows=1, ncols=6, figsize=(12, 6))
ax[0].plot(logs.GR, logs.Depth, '-g', alpha=0.8, lw = 0.9)
ax[1].plot(logs.ILD_log10, logs.Depth, '-b', alpha=0.8, lw = 0.9)
ax[2].plot(logs.DeltaPHI, logs.Depth, '-k', alpha=0.8, lw = 0.9)
ax[3].plot(logs.PHIND, logs.Depth, '-r', alpha=0.8, lw = 0.9)
ax[4].plot(logs.PE, logs.Depth, '-c', alpha=0.8, lw = 0.9)
im=ax[5].imshow(cluster, interpolation='none', aspect='auto',
cmap=cmap_facies,vmin=1,vmax=9)
divider = make_axes_locatable(ax[5])
cax = divider.append_axes("right", size="20%", pad=0.05)
cbar=plt.colorbar(im, cax=cax)
cbar.set_label((5*' ').join([' SS ', 'CSiS', 'FSiS',
'SiSh', ' MS ', ' WS ', ' D ',
' PS ', ' BS ']))
cbar.set_ticks(range(0,1)); cbar.set_ticklabels('')
for i in range(len(ax)-1):
ax[i].set_ylim(ztop,zbot)
ax[i].invert_yaxis()
ax[i].grid()
ax[i].locator_params(axis='x', nbins=3)
ax[0].set_xlabel("GR")
ax[0].set_xlim(logs.GR.min(),logs.GR.max())
ax[1].set_xlabel("ILD_log10")
ax[1].set_xlim(logs.ILD_log10.min(),logs.ILD_log10.max())
ax[2].set_xlabel("DeltaPHI")
ax[2].set_xlim(logs.DeltaPHI.min(),logs.DeltaPHI.max())
ax[3].set_xlabel("PHIND")
ax[3].set_xlim(logs.PHIND.min(),logs.PHIND.max())
ax[4].set_xlabel("PE")
ax[4].set_xlim(logs.PE.min(),logs.PE.max())
ax[5].set_xlabel('Facies')
ax[1].set_yticklabels([]); ax[2].set_yticklabels([]); ax[3].set_yticklabels([])
ax[4].set_yticklabels([]); ax[5].set_yticklabels([])
ax[5].set_xticklabels([])
f.suptitle('Well: %s'%logs.iloc[0]['Well Name'], fontsize=14,y=0.94)
data['Well Name'].unique()
['SHRIMPLIN', 'ALEXANDER D', 'SHANKLE', 'LUKE G U', 'KIMZEY A', 'CROSS H CATTLE', 'NOLAN', 'Recruit F9', 'NEWBY', 'CHURCHMAN BIBLE'] Categories (10, object): ['SHRIMPLIN', 'ALEXANDER D', 'SHANKLE', 'LUKE G U', ..., 'NOLAN', 'Recruit F9', 'NEWBY', 'CHURCHMAN BIBLE']
Call function to plot
make_facies_log_plot(
data[data['Well Name'] == 'SHRIMPLIN'],
facies_colors)
# plt.savefig("Well_example.png", dpi=400)
1-1-2 Histogram¶
We can use the Counter function to evaluate each class contribution quantitatively. To see facies frequency distribution we can use a bar plot as:
cn = Counter(data.FaciesLabels)
for i,j in cn.items():
percent = j / len(data) * 100
print('Class=%s, Count=%d, Percentage=%.3f%%' % (i, j, percent))
Class=FSiS, Count=780, Percentage=18.800% Class=CSiS, Count=940, Percentage=22.656% Class=PS, Count=686, Percentage=16.534% Class=WS, Count=582, Percentage=14.027% Class=D, Count=141, Percentage=3.398% Class=SiSh, Count=271, Percentage=6.532% Class=MS, Count=296, Percentage=7.134% Class=BS, Count=185, Percentage=4.459% Class=SS, Count=268, Percentage=6.459%
plt.bar(cn.keys(), cn.values(), color=facies_colors )
plt.title('Facies Distribution')
plt.ylabel('Frequency')
# plt.savefig("bar_plot.png", dpi=400)
Text(0, 0.5, 'Frequency')
This is imbalanced dataset. Dolomite has the lowest member participation. Comparing coarse siltstone, dolomite appears 8 times less than that.
1-1-3 Cross-plot¶
To visualize multiple pairwise bivariate distributions in a dataset, we may use the pairplot() function from the seaborn library. It shows the relationship for the combination of variables in the dataset in the matrix format with a univariate distribution plot in diagonal. It is clear that PE log has a non-linear relationship with average porosity. Other pairs do not show a clear pattern. The distribution pattern in diagonal shows that each label class (facies) with respect to each feature has acceptable separation although there is a strong overlap for various classes. The ideal pattern can be assumed as a clear separation of distribution plots in tall bell shape normal distribution graph.
sns_plot = sns.pairplot(data.drop(['Well Name','Facies','Formation','Depth','NM_M','RELPOS'],axis=1),
hue='FaciesLabels', palette=facies_color_map,
hue_order=list(reversed(facies_labels)))
sns_plot.savefig('cross_plots.png')
Hereafter we will store dataset into new vriable after main operations (indented paragrpahs in introduction).¶
data_fe = data
data_fe.isna().sum()
Facies 0 Formation 0 Well Name 0 Depth 0 GR 0 ILD_log10 0 DeltaPHI 0 PHIND 0 PE 917 NM_M 0 RELPOS 0 FaciesLabels 0 dtype: int64
# to find out which wells do not have PE
df_null = data_fe.loc[data_fe.PE.isna()]
df_null['Well Name'].unique()
['ALEXANDER D', 'KIMZEY A', 'Recruit F9'] Categories (3, object): ['ALEXANDER D', 'KIMZEY A', 'Recruit F9']
Here, PE has 917 null values.
There are several ways to deal with Null values in the dataset. The simplest approach is to drop the rows containing at least one null value. This can be logical with a bigger size dataset but in small data frames, single points are important. We can impute null values with mean or from adjacent data points in columns. Filling with mean value will not affect data variance and therefore will not have an impact on prediction accuracy, though can create data bias. Filling with the neighbor cells of column values can be appropriate if we have a geologically homogeneous medium like mass pure carbonate rocks.
Another approach, that I will implement here, to employe machine learning models to predict missing values. This is the best way of dealing with this dataset because we have just a single feature missing from the dataset, PE. On the other hand, filling with ML prediction is much better than the single mean value because we are able to see ML correlation and accuracy by dividing data to train and test sets.
data_fe.corr().style.background_gradient(cmap='coolwarm').set_precision(2)
| Facies | Depth | GR | ILD_log10 | DeltaPHI | PHIND | PE | NM_M | RELPOS | |
|---|---|---|---|---|---|---|---|---|---|
| Facies | 1.00 | 0.31 | -0.39 | 0.38 | -0.24 | -0.36 | 0.70 | 0.85 | 0.08 |
| Depth | 0.31 | 1.00 | -0.09 | 0.20 | 0.07 | -0.10 | 0.28 | 0.28 | 0.00 |
| GR | -0.39 | -0.09 | 1.00 | -0.21 | 0.18 | 0.27 | -0.29 | -0.32 | -0.18 |
| ILD_log10 | 0.38 | 0.20 | -0.21 | 1.00 | -0.10 | -0.54 | 0.38 | 0.49 | 0.09 |
| DeltaPHI | -0.24 | 0.07 | 0.18 | -0.10 | 1.00 | -0.19 | 0.01 | -0.18 | 0.02 |
| PHIND | -0.36 | -0.10 | 0.27 | -0.54 | -0.19 | 1.00 | -0.57 | -0.48 | -0.03 |
| PE | 0.70 | 0.28 | -0.29 | 0.38 | 0.01 | -0.57 | 1.00 | 0.66 | 0.02 |
| NM_M | 0.85 | 0.28 | -0.32 | 0.49 | -0.18 | -0.48 | 0.66 | 1.00 | 0.03 |
| RELPOS | 0.08 | 0.00 | -0.18 | 0.09 | 0.02 | -0.03 | 0.02 | 0.03 | 1.00 |
We can use various ML models to predict PE log as countinious regression problem. Here, I will employ Multi-Layer Percepteron Neural Network from scikit-learn to predict target value. I am not going to deep for this approach and use simply to predict missing values.
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn import linear_model
set_PE = data_fe[['Facies','Depth', 'GR', 'ILD_log10',
'DeltaPHI', 'PHIND', 'PE', 'NM_M', 'RELPOS']].dropna() # select features and target log that has value
X = set_PE[['Facies','Depth', 'GR', 'ILD_log10',
'DeltaPHI', 'PHIND', 'NM_M', 'RELPOS']] # feature selection without null value
XX = data_fe[['Facies','Depth', 'GR', 'ILD_log10',
'DeltaPHI', 'PHIND', 'NM_M', 'RELPOS']]
y = set_PE['PE'] # target log
# scaling
scaler = StandardScaler()
X = scaler.fit_transform(X)
X_b = scaler.fit_transform(XX)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
%%time
MLP_pe = MLPRegressor(random_state=1, max_iter= 500).fit(X_train, y_train) #fit the model
MLP_pe.score(X_test, y_test) # examine accuracy
Wall time: 3.1 s
0.776094801295609
data_fe['PE_pred'] = MLP_pe.predict(X_b) # predict PE
data_fe.PE.fillna(data_fe.PE_pred, inplace =True) # fill NaN vakues with predicted PE
Plot predecited PE¶
make_facies_log_plot(
data[data['Well Name'] == 'ALEXANDER D'],
facies_colors)
plt.savefig("predicted_PE.png", dpi=400)
Predicted PE in well ALEXANDER D shows the normal range and variation. Prediction accuracy is 77%.
# remove predicted PE column
data_fe = data_fe.drop(columns=['PE_pred'])
data = data.drop(columns=['PE_pred'])
1-2-2 Feature extraction¶
Having limited set of features in this dataset can lead us to think about extracting some data from existing dataset.
First, we can convert formation categorical data into numeric data. Our background knowledge can help us to predict that some facies are possibly presnet more in a specififc formation rather than others.
We can use the LabelEncoder function:
data_fe['Formation_num'] = LabelEncoder().fit_transform(data_fe['Formation'].astype('str')) + 1
f_num = pd.get_dummies(data_fe['Formation'], prefix='fm')
data_fe = pd.concat([data_fe,f_num ], axis=1, join="inner" )
We converted formation category data into numeric to use as a predictor and added 1 to start predictor from 1 instead of zero. To see if new feature extraction would assist prediction improvement, we should define a baseline model then compare it with the extracted feature model.
pd.set_option('display.max_columns', None)
data_fe.head()
| Facies | Formation | Well Name | Depth | GR | ILD_log10 | DeltaPHI | PHIND | PE | NM_M | RELPOS | FaciesLabels | fm_A1 LM | fm_A1 SH | fm_B1 LM | fm_B1 SH | fm_B2 LM | fm_B2 SH | fm_B3 LM | fm_B3 SH | fm_B4 LM | fm_B4 SH | fm_B5 LM | fm_B5 SH | fm_C LM | fm_C SH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | A1 SH | SHRIMPLIN | 2793.0 | 77.45 | 0.664 | 9.9 | 11.915 | 4.6 | 1 | 1.000 | FSiS | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 3 | A1 SH | SHRIMPLIN | 2793.5 | 78.26 | 0.661 | 14.2 | 12.565 | 4.1 | 1 | 0.979 | FSiS | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 3 | A1 SH | SHRIMPLIN | 2794.0 | 79.05 | 0.658 | 14.8 | 13.050 | 3.6 | 1 | 0.957 | FSiS | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 3 | A1 SH | SHRIMPLIN | 2794.5 | 86.10 | 0.655 | 13.9 | 13.115 | 3.5 | 1 | 0.936 | FSiS | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 3 | A1 SH | SHRIMPLIN | 2795.0 | 74.58 | 0.647 | 13.5 | 13.300 | 3.4 | 1 | 0.915 | FSiS | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
data_fe['Well Name'].unique()
['SHRIMPLIN', 'ALEXANDER D', 'SHANKLE', 'LUKE G U', 'KIMZEY A', 'CROSS H CATTLE', 'NOLAN', 'Recruit F9', 'NEWBY', 'CHURCHMAN BIBLE'] Categories (10, object): ['SHRIMPLIN', 'ALEXANDER D', 'SHANKLE', 'LUKE G U', ..., 'NOLAN', 'Recruit F9', 'NEWBY', 'CHURCHMAN BIBLE']
Pick up a well as blind:¶
machine learning algorithm will not see this data in the training process. We will use it at the end to see how the model works. Remember to select a well that includes all types of facies classes, otherwise in prediction, data dimension inconsistency will generate an error. Or simply add a lacking facies example to the well to avoid the problem.
blind = data_fe[data_fe['Well Name'] == 'KIMZEY A']
data_fe = data_fe[data_fe['Well Name'] != 'KIMZEY A']
To see if new feature extraction would assisst prediction improvment, we should define a baseline model then compare with extracted feature model.
Baseline Model Performance¶
For simplicity, we will use a logistic regression classifier as a baseline model and will examine model performance with a cross-validation concept. Data will be split into 10 subgroups and the process will be repeated 3 times.
y = data_fe.pop('Facies')
X = data_fe.drop(columns=['Formation', 'Well Name', 'FaciesLabels'])
from numpy import mean
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
For simplicity we will use logistic regression classifier as baseline model and will examine model performance with cross validation concept. Data will be splitted into 10 subgroups and process will be reapeted 3 times.
model = LogisticRegression(solver='liblinear')
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate model
scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
print('Accuracy: %.3f' % (mean(scores)))
Accuracy: 0.593
Here, we can explore whether feature extraction can improve model performance. There are many aprroaches while we will use some transforms for chaining the distribution of the input variables such as Quantile Transformer and KBins Discretizer. Then, will remove linear dependecies between the input variables using PCA and TruncatedSVD.
To study more refer here.
Using feature union class, we will define list of transforms to perform results aggrigated together. This will create a dataset with lots of feature columns while we need to reduce dimentionality to faster and better performance. Finally, Recursive Feature Elimination, or RFE, technique can be used to select the most relevent features. We select 30 features.
%%time
from sklearn.pipeline import Pipeline
from sklearn.pipeline import FeatureUnion
from sklearn.preprocessing import RobustScaler
from sklearn.preprocessing import QuantileTransformer
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.decomposition import TruncatedSVD
from sklearn.feature_selection import RFE
from sklearn.decomposition import PCA
#-------------------------------------------------- append transforms into a list
transforms = list()
transforms.append(('qt', QuantileTransformer(n_quantiles=100, output_distribution='normal')))
transforms.append(('kbd', KBinsDiscretizer(n_bins=10, encode='ordinal', strategy='uniform')))
transforms.append(('pca', PCA(n_components=7)))
transforms.append(('svd', TruncatedSVD(n_components=7)))
#-------------------------------------------------- initialize the feature union
fu = FeatureUnion(transforms)
#-------------------------------------------------- define the feature selection
rfe = RFE(estimator=LogisticRegression(solver='liblinear'), n_features_to_select=30)
#-------------------------------------------------- define the model
model = LogisticRegression(solver='liblinear')
#-------------------------------------------------- use pipeline to chain operation
steps = list()
steps.append(('fu', fu))
steps.append(('rfe', rfe))
steps.append(('ml', model))
pipeline = Pipeline(steps=steps)
# define the cross-validation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate model
scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# report performance
print('Accuracy: %.3f' % (mean(scores)))
Accuracy: 0.613 Wall time: 1min 39s
Accuracy improvement shows that feature extraction can be useful approach when we are dealing with limited features in dataset.
1-2-3 Oversampeling¶
In imbalanced datasets, we can use resampling technique to add some more data point to increase members of minority groups. This can be helpful whenever minority label targets has special importance such as credit card fraud detection. In that example, fraud can happen with less than 0.1 percent of transaction while it is important to detect fraud.
In this work, we will add psudo observation for Dolomite class which has the lowest poulation
Synthetic Minority Oversampling Technique, SMOTE: the technique is used to select nearest neighbors in the feature space, separated examples by adding a line and producing new examples along the line. The method is not merely generating the duplicates from the outnumbered class, but applied K-nearest neighbours to generate synthetic data.
#!pip install imblearn
from imblearn.over_sampling import SMOTE
smote = SMOTE()
X_sm1 , y_sm1 = smote.fit_resample(X,y)
X_sm , y_sm = X_sm1 , y_sm1 # keep for fuuture plotting an cimparision
print("Before SMOTE: ", Counter(y))
print("After SMOTE: ", Counter(y_sm))
Before SMOTE: Counter({2: 855, 3: 706, 8: 596, 6: 531, 1: 259, 5: 243, 4: 228, 9: 178, 7: 114})
After SMOTE: Counter({3: 855, 2: 855, 8: 855, 6: 855, 7: 855, 4: 855, 5: 855, 9: 855, 1: 855})
Now, dataset is balanced. Let's see how works comparing Baseline model:
scaler = StandardScaler()
X_sm = scaler.fit_transform(X_sm)
model_bal = LogisticRegression(solver='liblinear')
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate model
scores = cross_val_score(model_bal, X_sm, y_sm, scoring='accuracy', cv=cv, n_jobs=-1)
print('Accuracy: %.3f' % (mean(scores)))
Accuracy: 0.652
Accuracy improved by 3 percent but in multi-class classification, accuracy is not the best evaluation metrics. We will cover others in next parts.
data_fi = data
The concept is simple: features have higher correlation coefficient with target values are important for prediction. We can extract these coef's like:
# logistic regression for feature importance
from sklearn.datasets import make_classification
from sklearn.linear_model import LinearRegression
from matplotlib import pyplot
# define dataset
model = LinearRegression()
# fit the model
model.fit(X, y)
# get importance
importance = model.coef_
# summarize feature importance
for i,v in enumerate(importance):
print('Feature: %0d, Score: %.5f' % (i,v))
# plot feature importance
pyplot.bar([x for x in range(len(importance))], importance)
pyplot.title('Logistic Regression Coefficients as Feature Importance Scores')
pyplot.savefig('reg_importance.png')
pyplot.show()
Feature: 0, Score: 0.00106 Feature: 1, Score: -0.00753 Feature: 2, Score: 0.26791 Feature: 3, Score: -0.01909 Feature: 4, Score: 0.04268 Feature: 5, Score: 0.67395 Feature: 6, Score: 1.72536 Feature: 7, Score: 0.30698 Feature: 8, Score: 0.46538 Feature: 9, Score: -0.88411 Feature: 10, Score: 1.24697 Feature: 11, Score: -1.11251 Feature: 12, Score: 1.28419 Feature: 13, Score: -1.10428 Feature: 14, Score: 1.47229 Feature: 15, Score: -1.07719 Feature: 16, Score: 0.91050 Feature: 17, Score: -1.46548 Feature: 18, Score: 1.61115 Feature: 19, Score: -0.58955 Feature: 20, Score: 0.18510 Feature: 21, Score: -0.94244
1-3-2 Decision tree¶
This algorithm provides importance scores based on the reduction in the criterion used to split in each node such as entropy or Gini.
from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier()
# fit the model
model.fit(X, y)
# get importance
importance = model.feature_importances_
# summarize feature importance
for i,v in enumerate(importance):
print('Feature: %0d, Score: %.5f' % (i,v))
# plot feature importance
pyplot.bar([x for x in range(len(importance))], importance)
pyplot.title('Decision tree classifier Feature Importance Scores')
pyplot.savefig('DTree.png')
pyplot.show()
XGBoost is a library that provides an efficient and effective implementation of the stochastic gradient boosting algorithm. This algorithm can be used with scikit-learn via the XGBRegressor and XGBClassifier classes.
#pip install xgboost
from xgboost import XGBClassifier
model = XGBClassifier()
# fit the model
model.fit(X, y)
# get importance
importance = model.feature_importances_
# summarize feature importance
for i,v in enumerate(importance):
print('Feature: %0d, Score: %.5f' % (i,v))
# plot feature importance
pyplot.bar([x for x in range(len(importance))], importance)
pyplot.title('XGBoost classifier Feature Importance Scores')
pyplot.show()
1-3-3 Permutation feature importance¶
Permutation feature importance is a model inspection technique that can be used for any fitted estimator when the data is tabular. This is especially useful for non-linear or opaque estimators. The permutation feature importance is defined to be the decrease in a model score when a single feature value is randomly shuffled.
from sklearn.inspection import permutation_importance
model = LogisticRegression(solver='liblinear')
# fit the model
model.fit(X, y)
# perform permutation importance
results = permutation_importance(model, X, y, scoring='accuracy')
# get importance
importance = results.importances_mean
# summarize feature importance
for i,v in enumerate(importance):
print('Feature: %0d, Score: %.5f' % (i,v))
# plot feature importance
pyplot.bar([x for x in range(len(importance))], importance)
pyplot.title('Permutation Feature Importance Scores')
pyplot.savefig('permu.png')
pyplot.show()
In all these feature importance plots we can see that predictor number 6 (PE log) has the most importance in label prediction. Based on the model that we select to evaluate the result, we may choose features based on their importance and neglect the rest to speed up the training process. This is very common if we are rich in feature quantity, though in our example dataset here, we will use all features as predictors are limited.
The philosophy of constructing a baseline model is simple: we need a basic and simple model to see how the adjustments on both data and model parameters can cause improvement in model performance. In fact, this is like a scale for comparison.
In this code script, we first defined our favorite model classifiers. Then, established baseline_model function. In this function, we employed the Pipeline function to implement step wised operation of data standard scaling(facilitate model running more efficient) and model object calling for cross-validation. I like Pipeline because it makes the codes more tidy and readable.
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import ExtraTreesClassifier
# define Classifiers
log = LogisticRegression()
knn = KNeighborsClassifier()
dtree = DecisionTreeClassifier()
rtree = RandomForestClassifier()
svm = SVC()
nb = GaussianNB()
gbc = GradientBoostingClassifier()
etree = ExtraTreesClassifier()
Define a function that uses pipeline to impelement data transformation and fit with model then cross validate
def baseline_model(model_name):
model = model_name
steps = list()
steps.append(('ss', StandardScaler() ))
steps.append(('ml', model))
pipeline = Pipeline(steps=steps)
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# balanced X,y from SMOTE can also be used
scores = cross_val_score(pipeline, X_sm, y_sm, scoring='accuracy', cv=cv, n_jobs=-1)
print(model,'Accuracy: %.3f' % (mean(scores)))
Run functions
%%time
baseline_model(log)
baseline_model(knn)
baseline_model(dtree)
baseline_model(rtree)
baseline_model(svm)
baseline_model(nb)
baseline_model(gbc)
baseline_model(etree)
LogisticRegression() Accuracy: 0.664 KNeighborsClassifier() Accuracy: 0.872 DecisionTreeClassifier() Accuracy: 0.850 RandomForestClassifier() Accuracy: 0.916 SVC() Accuracy: 0.746 GaussianNB() Accuracy: 0.318 GradientBoostingClassifier() Accuracy: 0.850 ExtraTreesClassifier() Accuracy: 0.930 Wall time: 49.6 s
Cross-validation#:~:text=Cross%2Dvalidation%2C%20sometimes%20called%20rotation,to%20an%20independent%20data%20set.) sometimes called rotation estimation or out-of-sample testing is any of the various similar model validation techniques for assessing how the results of a statistical analysis will generalize to an independent data set. Models usually are overfitting when the accuracy score on training data is much higher than testing data. One way to examine model performance is to keep randomly some part of the dataset hold-out. This can be a weakness for small datasets. Another way is to divide the dataset into splits and run it while each split has a different set of test folds like the picture below. In this approach, cross-validation, models can examine all data without overfitting. However, for this project, we will keep a single well as a hold-out to examine model performances after all optimizations.
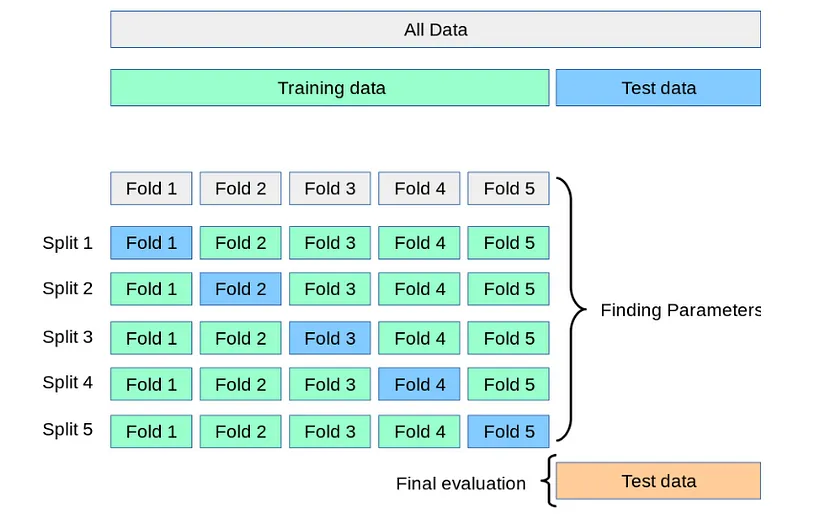 picture from scikit-learn
picture from scikit-learn
We repeated 3 times each operation over a dataset that already divided into 10 equal parts(folds) in cross-validation. In fact, we intended to expose the model to all data with a different combination of train and test sets without overlap.
Here, we used an average of accuracy as metrics for comparison of various model performances(accuracy and other evaluation metrics will be elaborated in the next post). It is used for simplicity, while for multi-class classification problems, accuracy is the weakest model evaluation approach. We will cover model evaluation metrics for multi-class classification problems in the next posts.
The Extra tree and Random forest classifier showed the best accuracy score for the facies label prediction while the Gaussian Naive Bayes classifier performed poorly.
We created a baseline model in the previous section without adjucting hyper-parameters (parameters that are adjustable by user). Sometimes, careful selection of these parameters can improve model results noticeably. Grid search is designed to employ numeric/string range for specific hyper parameter without having to code loop functions.
from sklearn.model_selection import GridSearchCV
X_train, X_test, y_train, y_test = train_test_split(X_sm, y_sm, test_size=0.2, random_state=42)
%%time
#logistic regression classifier
#define hyper parameters and ranges
param_grid_log = [{'C': [0.1, 1, 10], 'solver': ['lbfgs', 'liblinear'],
'max_iter':[100, 300]}]
#apply gridsearch
grid_log = GridSearchCV(log, param_grid=param_grid_log, cv=5)
#fit model with grid search
grid_log.fit(X_train, y_train)
print('The best parameters for log classifier: ', grid_log.best_params_)
The best parameters for log classifier: {'C': 10, 'max_iter': 300, 'solver': 'lbfgs'}
Wall time: 12.5 s